删除 '_posts/go-5.md'

_posts/go-5.md

@@ -1,401 +0,0 @@
----
-title: golang 六个比较排序算法实现
-date: 2020-07-03 10:00:00
-tags: Golang
-cover: https://static.jqwei.com/blog/img/IMG_3459.PNG
-categories: 编程语言
----
-### golang 比较排序算法实现
-
-* [比较排序算法](#-1)
-  - [交换排序](#-14)
-    + [冒泡排序](#-16)
-    + [快速排序](#-37)
-  - [插入排序](#-88)
-    + [简单插入排序](#-90)
-    + [希尔排序](#-116)
-  - [选择排序](#-151)
-    + [简单选择排序](#-153)
-    + [堆排序](#-178)
-
-# 比较排序算法
-
-这里的比较排序算法重点并非比较算法之间优劣，这里的比较一词指的是接下来讲的六种排序算法皆为通过比较来决定元素次序。
-
-比较排序 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 是否稳定
-_**交换排序**_
-
-冒泡排序 O(n²) O(n²) O(n) O(1) 稳定 快速排序 O(nlog₂n) O(n²) O(nlog₂n) O(nlog₂n) 不稳定
-_**插入排序**_
-
-简单插入排序 O(n²) O(n²) O(n) O(1) 稳定 希尔排序 O(n3/2) O(n²) O(n) O(1) 不稳定
-_**选择排序**_
-
-简单选择排序 O(n²) O(n²) O(n²) O(1) 不稳定 堆排序 O(nlog₂n) O(nlog₂n) O(nlog₂n) O(1) 不稳定
-
-## 交换排序
-
-所谓交换，就是根据序列中两个记录键值的比较结果来互换这两个记录在序列中的位置。
-
-### 冒泡排序
-
-冒泡算是最简单的交换排序了。具体步骤如下：
-
-1. 通过循环获取一个未排序元素
-2. 将该元素循环比较一个未排序元素，符合排序条件(更大或更小)则交换，直到元素全部对比过，此时该元素即为当前循环中的最大/最小元素。
-3. 重复步骤1-2直到所有元素均为排序后元素。
-
-golang实现
-
-```go
-func BubbleSort(array []int) {
-
-	for i := 0; i < len(array); i++ {
-
-		for j := i + 1; j < len(array); j++ {
-			if array[i] > array[j] {
-				array[i], array[j] = array[j], array[i]
-			}
-		}
-	}
-}
-```
-
-### 快速排序
-
-快排是冒泡排序的改良版，也是极为常用的排序手段，golang标准库中的排序就使用了快排。具体步骤如下：
-
-1. 设定一个分界值x，通过该分界值将数组分成左右两部分（这里我们简单的把分界值设成第一个元素）。
-2. 从右边开始循环判断是否比分界值更小，如果更小则把该值填入当前 i 的位置并退出循环，否则继续循环
-3. 从左边开始循环判断是否比分界值更大，如果更大则把该值填入当前 j 的位置并退出循环，否则继续循环
-4. 重复2-3，直至i
-
-golang实现
-
-```go
-
-func doPivot(array []int, left, right int) {
-	if left < right {
-		i := left
-		j := right
-		x := array[left]
-		for i < j {
-			for i < j {
-				if array[j] < x {
-					array[i] = array[j]
-					i++
-					break
-				} else {
-					j--
-				}
-			}
-			for i < j {
-				if array[i] > x {
-					array[j] = array[i]
-					j--
-					break
-				} else {
-					i++
-				}
-			}
-		}
-		array[i] = x
-		doPivot(array, left, i-1)
-		doPivot(array, i+1, right)
-	}
-}
-
-func QuickSort(array []int) {
-	left := 0
-	right := len(array) - 1
-	doPivot(array, left, right)
-}
-```
-
-## 插入排序
-
-所谓插入，指的就是将未排序元素插入有序的队列。
-
-### 简单插入排序
-
-简单插入排序的实现非常简单。具体步骤如下：
-
-1. 循环获取未排序的元素，该元素设为current(当前元素）
-2. 将当前元素循环对比排序后队列，符合排序条件(更大或更小)则将那个对比元素后移一位
-3. 不符合排序条件则停止循环并将值插入进队列
-4. 重复步骤1-3直到所有元素均为排序后元素。
-
-golang实现
-
-```go
-func InsertionSort(array []int) {
-	var preIndex, current int
-
-	for i := 1; i < len(array); i++ {
-		preIndex = i - 1
-		current = array[i]
-
-		for preIndex >= 0 && current < array[preIndex] {
-			array[preIndex+1] = array[preIndex]
-			preIndex--
-		}
-		array[preIndex+1] = current
-	}
-}
-```
-
-### 希尔排序
-
-希尔排序是简单插入排序算法的一种更高效的改进版本，主要是在简单插入排序的基础上增加了增量的概念，减少了其复制的次数，golang标准库中的排序就使用了希尔排序。具体步骤如下：
-
-1. 设置增量step（这里我们设置为长度/2，不管你自己设成什么规则最后一次增量都应该为1），循环增量序列
-2. 根据增量序列的每一次增量值为初始下标来获取循环队列（step，len(array)）
-3. 设 前值下标 为 当前下标-增量值
-4. 循环对比当前值与前值，若符合排序条件(大于/小于)则更新对应前值下标与当前值下标并继续循环，否则跳出循环
-5. 将当前值插入队列对应位置
-6. 循环3-4直至增量
-
-其实这里的步骤2-5就是一个简单插入循环，只不过这里加入了一个增量序列，从对比上一个值变成了对比上一个增量下标的值。
-
-golang实现
-
-```go
-func ShellSort(array []int) {
-
-	for step := len(array) / 2; step >= 1; step = step / 2 {
-
-		for i := step; i < len(array); i++ {
-			currentIndex := i
-			preIndex := currentIndex-step
-			current := array[i]
-
-			for j-step >= 0 && current < array[preIndex] {
-				array[currentIndex] = array[preIndex]
-				currentIndex = currentIndex - step
-				preIndex = currentIndex-step
-			}
-			array[j] = current
-		}
-	}
-}
-```
-
-## 选择排序
-
-所谓选择，就是将最符合排序条件(最大或最小)的元素一个个拿出来。
-
-### 简单选择排序
-
-简单选择排序应该是选择排序中最简单的实现。具体步骤如下：
-
-1. 循环获取未排序的元素，该元素的下标设为极值(最大或最小)
-2. 循环对比未排序元素，获得极值下标。
-3. 将极值下标对应元素与1中获取的原始极值的元素进行交换
-4. 重复步骤1-3直到所有元素均为排序后元素。
-
-```go
-func SelectionSort(array []int) {
-	var minIndex int
-
-	for i := 0; i < len(array)-1; i++ {
-		minIndex = i
-
-		for j := i + 1; j < len(array); j++ {
-			if array[j] < array[minIndex] {
-				minIndex = j
-			}
-		}
-
-		array[i], array[minIndex] = array[minIndex], array[i]
-	}
-}
-```
-
-### 堆排序
-
-推排序指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点，它同时属于选择排序的一种（将最大堆节点或最小堆节点选择出来），golang标准库中的排序就使用了堆排序。具体步骤如下：
-
-1. 在顶部构建最大元素的堆
-（1）从最后一个拥有子节点的父节点开始往上实现父元素更大堆属性
-2. 最大的元素放置末尾
-（1）将未排序队列中的最大元素放置末尾
-（2）使未排序队列实现父元素更大堆属性
-
-实现父元素更大堆属性的具体步骤如下：
-
-1. 循环父节点下的所有子节点
-2. 判断父节点是否存在子节点，若不存在子节点退出循环
-3. 判断两个子节点哪个更大，选择大的那一个子节点
-4. 判断父节点是否大于子节点，若大于则退出循环
-5. 互换父子节点
-6. 将子节点设为父节点重新循环
-
-该实现其实就是golang标准库下排序中的堆排序实现，只不过由于在Sort中堆排序只是其排序逻辑中的一部分，因此具有一些其他与堆排序无关的属性，在此将其删除。
-
-```go
-func siftDown(array []int, lo, hi int) {
-	rootIndex := lo
-
-	for {
-		childIndex := 2*rootIndex + 1
-
-		if childIndex >= hi {
-			break
-		}
-
-		if childIndex+1 < hi && array[childIndex]  array[childIndex+1] {
-			childIndex++
-		}
-
-		if array[rootIndex] > array[childIndex] {
-			break
-		}
-
-		array[rootIndex], array[childIndex] = array[childIndex], array[rootIndex]
-		rootIndex = childIndex
-	}
-}
-
-func HeapSort(array []int) {
-	lo := 0
-	hi := len(array)
-
-	for i := (hi - 1) / 2; i >= 0; i-- {
-
-		siftDown(array, i, hi)
-	}
-
-	for i := hi - 1; i >= 0; i-- {
-
-		array[0], array[i] = array[i], array[0]
-
-		siftDown(array, lo, i)
-	}
-}
-```
-
-仅看代码的情况下如果你对堆的数据结构不怎么了解或许你还是会比较懵，因此我就用图来举个例子，剩下的过程你自己试验一下看一遍流程立马就懂了。
-
-现调用HeapSort函数并传入一个int切片
-
-```go
-HeapSort([]int{5, 4, 6, 7, 0, 3, 4, 8, 2, 9})
-```
-
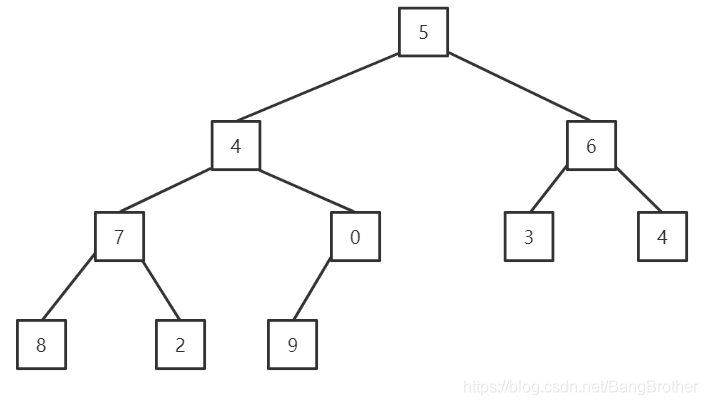
-此时切片[]int{5, 4, 6, 7, 0, 3, 4, 8, 2, 9}转换为堆的效果就是
-![](https://img-blog.csdnimg.cn/20200623112033513.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0JhbmdCcm90aGVy,size_16,color_FFFFFF,t_70)
-当程序运行至
-
-```go
-
-	for i := (hi - 1) / 2; i >= 0; i-- {
-
-		siftDown(array, i, hi)
-	}
-```
-
-第一次循环 i = (10-1)/2这个 i 就是最后一个具有子节点的父节点下标4，array[4]=0，看上图array[4]符合条件。
-进入 `siftDown(array,4,10)`函数
-
-```go
-childIndex := 2*rootIndex + 1
-```
-
-这里的 `2*rootIndex + 1`公式对应着父节点的第一个子节点下标此时为9，
-
-```go
-if childIndex >= hi {
-	break
-}
-```
-
-9小于堆的最大长度10，则存在该子节点，循环继续。
-
-```go
-if childIndex+1 < hi && array[childIndex]  array[childIndex+1] {
-	childIndex++
-}
-```
-
-9+1并不小于最大长度10，不存在下一个兄弟节点，跳过if判断，循环继续。
-
-```go
-if array[rootIndex] > array[childIndex] {
-	break
-}
-array[rootIndex], array[childIndex] = array[childIndex], array[rootIndex]
-rootIndex = childIndex
-
-```
-
-4<9，父节点并不大于子节点，因此将其互换并将子节点设为父节点继续循环
-```go
-childIndex := 2*rootIndex + 1
-if childIndex >= hi {
-	break
-}
-1
-2
-3
-4
-```
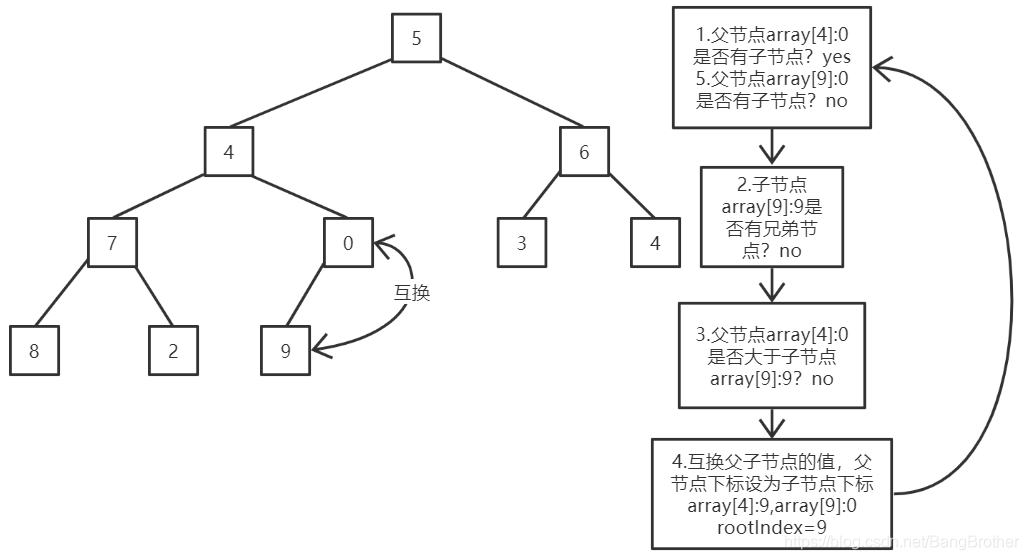
-下标9的子节点下标为19，大于堆的长度10，不存在该子节点退出循环。
-array此时为[5, 4, 6, 7, 9, 3, 4, 8, 2, 0]
-
-逼逼赖赖这么多不如放张图：
-
-![](https://img-blog.csdnimg.cn/20200623115400581.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0JhbmdCcm90aGVy,size_16,color_FFFFFF,t_70)
-
-图实在是占地方了，后续循环我就不放图了，给你们个结果切片[]int自己转换，看一看就懂了。
-
-初始值 [5 4 6 7 0 3 4 8 2 9]
-
-
-调用siftDown(array, 4 , 10 )
-
-交换后结果 [5 4 6 7 9 3 4 8 2 0] 继续循环
-
-rootIndex: 9 没有子节点退出循环
-
-
-调用siftDown(array, 3 , 10 )
-
-交换后结果 [5 4 6 8 9 3 4 7 2 0] 继续循环
-
-rootIndex: 7 没有子节点退出循环
-
-
-调用siftDown(array, 2 , 10 )
-
-child兄弟节点更大，选择该兄弟节点childIndex: 6
-
-父节点比子节点大退出循环
-
-
-
-调用siftDown(array, 1 , 10 )
-
-child兄弟节点更大，选择该兄弟节点childIndex: 4
-
-交换后结果 [5 9 6 8 4 3 4 7 2 0] 继续循环
-
-父节点比子节点大退出循环
-
-
-调用siftDown(array, 0 , 10 )
-
-交换后结果 [9 5 6 8 4 3 4 7 2 0] 继续循环
-
-交换后结果 [9 8 6 5 4 3 4 7 2 0] 继续循环
-
-交换后结果 [9 8 6 7 4 3 4 5 2 0] 继续循环
-
-rootIndex: 7 没有子节点退出循环
-
-最后获取得的 [9 8 6 7 4 3 4 5 2 0] 就是大顶堆，父节点皆比子节点大。
-
-排序我就不举例了，都是一个意思。如果还看不懂就把切片换成堆结构你就明白了。
-
-
-
-> 原文链接：https://blog.csdn.net/BangBrother/java/article/details/106866823